近年、ディープラーニングや敵対的生成ネットワークといった様々な機械学習手法が生み出され、日々進化を遂げています。これらのような最先端の機械学習に興味を持ってプログラミングを始めた方も多いですよね。
最新の機械学習を学ぶにあたって、基礎となる機械学習手法について学ぶことは非常に重要です。基礎を理解しないと、最先端の機械学習手法を応用することもできません。
機械学習手法の基礎として学ぶのにオススメなのが、サポートベクトルマシン(SVM)。サポートベクトルマシン(SVM)は、与えられたデータをその特徴によって2つに分類する手法です。
また、サポートベクトルマシン(SVM)自体の分類性能は数ある機械学習手法の中でも非常に優秀で、機械学習の最も有名なコンテストであるkaggleにおいても上位入賞者が頻繁に利用するほどです。
サポートベクトルマシン(SVM)の原理について理解すると、機械学習はどのようにしてデータを分類しているのかの学習過程を理解できるでしょう。この知識は今後、他の機械学習手法を学ぶ際にも非常に重要に違いありません。
そこで今回は、機械学習手法の基礎として、サポートベクトルマシン(SVM)について解説します。
サポートベクトルマシン(SVM)って何?


サポートベクトルマシン(SVM)とは、教師あり学習による2クラス分類の機械学習手法です。教師あり学習とは、答えが紐付いた問題をプログラムに与え、プログラムが計算した答えと用意した答えが近づくようプログラム内のパラメータを調整することで学習するタイプの機械学習手法です。
また2クラス分類というのは、与えたデータの特徴を判断して2つのグループに分類すること。例えば、人の顔写真の特徴から男の人の写真と女の人の写真に分類するのがこれに当たります。
では実際に、サポートベクトルマシン(SVM)の動作を簡単に説明しましょう。xy平面上に散らばった、たくさんの点を想像してください。これらの点の内、半分は平面の右側に、もう半分は平面の左側に位置しています。サポートベクトルマシン(SVM)は、「カーネル法」や「マージン最大化」という考え方を使って、これらの点をうまく分けられるような直線を決定することができます。「カーネル法」「マージン最大化」については、後ほど詳しく解説します。
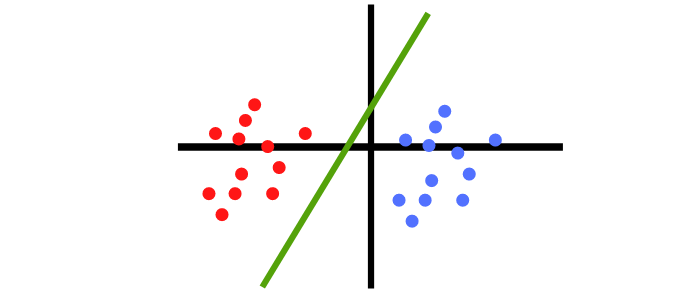

サポートベクトルマシンの特徴


サポートベクトルマシン(SVM)はデータを2つに分類する機械学習手法の中で現在最も精度が高いと言われています。もう一度、xy平面の内、右側にある点群と左側にある点群をイメージしましょう。
これらの点群を分けることができる直線は無数に存在します。これは直線の傾きを変えたり、直線の位置を片側の点群ギリギリまで寄せることもできるためです。
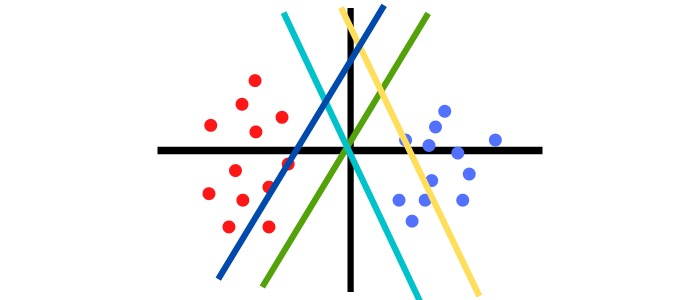

サポートベクトルマシン(SVM)のすごい点は、理論的に直線の傾きや位置を最適化できる点です。これによって、本来属している点群から少し離れたデータであっても正しく分類できる確率が大きく向上し、2クラス分類の機械学習で最高の性能を誇っています。
このように、2クラス分類では非常に優秀なサポートベクトルマシン(SVM)ですが、そのままではデータを3つ以上のグループに分類する「他クラス分類」には利用できないという欠点もあるので、自分がどのような問題を解きたいのかをしっかり考慮し、機械学習手法を選ぶようにしましょう。
カーネル法ついて


これまで、サポートベクトルマシン(SVM)は平面上の2つの点群をうまく分類するような直線を見つける手法でしたが、実は「カーネル法」という手法が取り入れると、直線でなく曲線での分割も可能です。
例えば今回は、平面上に位置している4つの点群を想像しましょう。点群はそれぞれ右上、右下、左上、左下の4箇所に分布しており、右上と左下の点群をAグループ、それ以外をBグループとします。
このままでは、Aグループの点群とBグループの点群にうまく分けられるような直線を書くことはできません。そこで登場するのがカーネル法です。
カーネル法は平面自体を捻じ曲げ、新しい平面を作り上げます。厳密ではありませんが、例えばカーネル法で先ほどの平面の右下と左下を入れ替えて新しい平面を作ったとしましょう。すると、Aグループの点群はすべて平面の右側に、Bグループの点群はすべて平面の左側に移動しました。
これによって新しい平面上ではAグループとBグループを分ける直線を書くことができます。
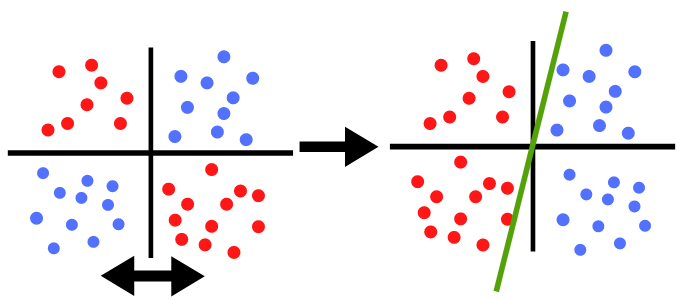

それではこの直線は、カーネル法を使用する前の平面に戻してみましょう。すると、元の平面ではAグループとBグループをうまく分割する曲線になっています。
このように、カーネル法を利用するとサポートベクトルマシン(SVM)によって平面上のデータを直線だけではなく曲線で分割することができ、様々な問題に対応できるようになりました。
マージン最大化とは


サポートベクトルマシン(SVM)の分類精度の向上に大きく寄与している仕組みの一つとして、マージン最大化という手法があります。
また、平面上の2つの点群(Aグループ、Bグループ)を想像します。この2つの点群を分割する直線を書くとき、普通にすると2つの点群のちょうど真ん中を通るような直線を書くことでしょう。これがマージン最大化です。
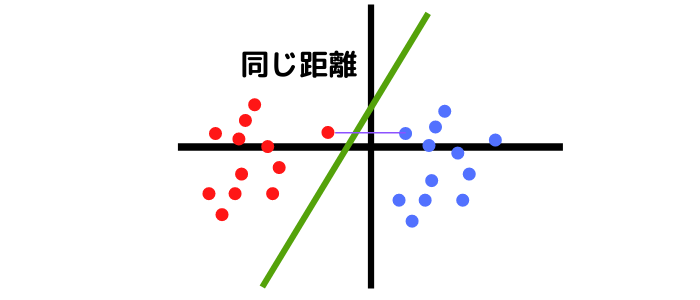

サポートベクトルマシン(SVM)では、Aグループのうち最もBグループに近い点と、Bグループの内最もAグループに近い点の真ん中を通るような直線を書きます。
これによって、書かれた直線と各グループの距離であるマージンを確保することができ、点群からはみ出たデータに対しても正しく分類できる確率を上げました。
ソフトマージンとハードマージンとは


ここまで、平面上の右側に位置する点群(Aグループ)と左側に位置する点群(Bグループ)のように、2つの点群が明確に分けられるような場合を考えました。このような点群の関係に対する分類方法をハードマージンと呼びます。
サポートベクトルマシン(SVM)におけるハードマージンに対するソフトマージンの変更点は、点群を分割する直線が少しくらい分割に失敗してもOKとしていることです。これによって少しは分類ミスが発生しますが、ほとんどの場合においてはうまく分類できるようにしています。
サポートベクトルマシンのポイント


最後にサポートベクトルマシン(SVM)を利用した機械学習を実施するにあたって、最も重要なポイントを紹介します。
それは、機械学習するデータを整理する前処理の段階で同じグループのデータ同士が似た値をとるようにすることです。この処理により、サポートベクトルマシンがデータの特徴を捉えやすくなって学習の精度が向上します。
このような前処理を行い、グループごとの特徴を際立たせることができれば、サポートベクトルマシンの精度はグッと上がることでしょう。


さて、今回はサポートベクトルマシンの基礎について解説しました。内容をまとめると、下記のようになります。
- サポートベクトルマシン(SVM)とは、教師あり学習による2クラス分類の機械学習手法
- サポートベクトルマシン(SVM)は2つの点群をうまく分けられる直線を自動的に見つける働きをする
- サポートベクトルマシン(SVM)はよる2クラス分類の機械学習で最も優秀
- カーネル法を利用することで、直線だけでなく曲線での分割も行える
- マージン最大化とは、2つの点群の中央を通るような直線を選ぶ方法
- 適切な前処理で分類しやすいデータを用意することが最も重要
サポートベクトルマシンは、他の機械学習手法と比べて比較的わかりやすく、導入しやすいにも関わらず精度が高いという特徴があります。このため、現実の問題を高い精度で解くことが求められるような際に用いられることが多く、機械学習をしていく上で非常に重要な手法であることは間違いありません。
みなさんもぜひ、サポートベクトルマシン(SVM)をマスターしましょう!
参考元
verum ipsum factum
静岡理工科大学情報学部コンピュータシステム学科・知能インタラクション研究室
AVINTON


