機械学習には学習手法の違いによる様々なアルゴリズムがありますよね。本記事ではそのアルゴリズムの中でも著名なサポートベクターマシン(SVM)について解説していきましょう。
サポートベクターマシン(SVM)とは
サポートベクターマシンは著名な機械学習アルゴリズムのひとつで、2クラス分類の線形識別関数を構築する手法です。複数クラス分類を行う場合はk-1個の1対他のサポートベクターマシンを構築することで対応します。
サポートベクターマシンの特徴としては、以下のような点があげられるでしょう。
- マージン最大化を行うため比較的汎化性能が高い
- カーネル関数を利用することで非線型なデータに対しても識別が可能
現在は勾配ブースティングや深層学習のようなアルゴリズムが流行していますが、それ以前に流行していたのがこのサポートベクターマシンで、数学的にきれいに問題を解くことができることから人気のあった手法です。
サポートベクターマシン(SVM)の学習アルゴリズム
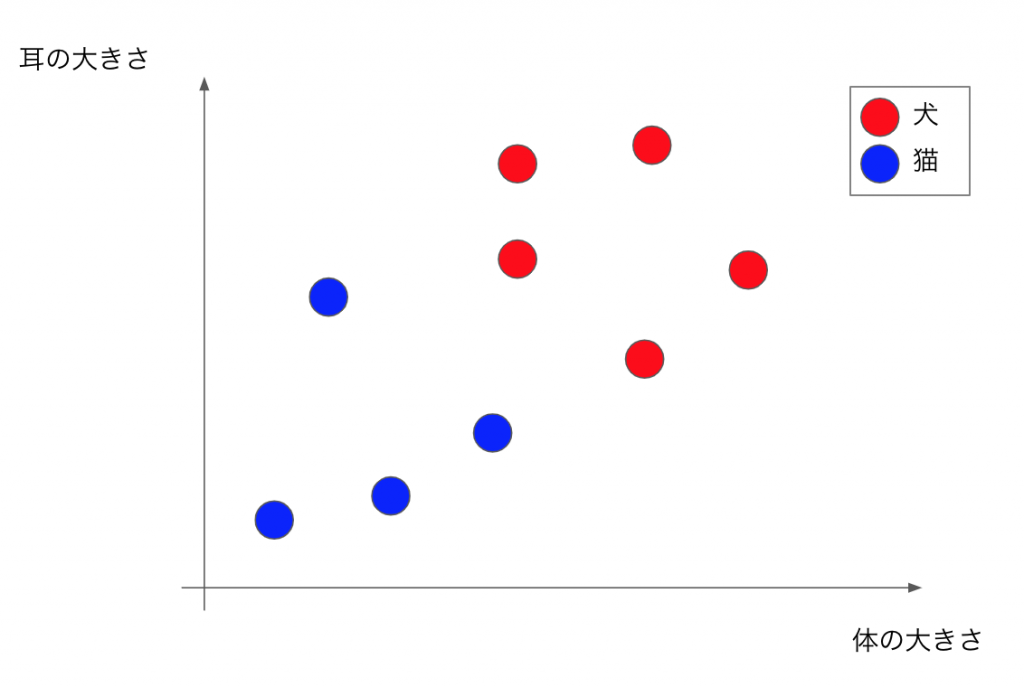

さて、ここからはサポートベクターマシン(SVM)の学習アルゴリズムについて理解するために、体の大きさと耳の大きさから犬と猫を識別するアルゴリズムの学習を考えてみましょう。
犬と猫を識別する境界を図中のどこに引くかをデータから学習させます。サポートベクターマシンでは「マージン最大化」という考えに基づきどのように境界を引くかを決定します。この境界を決定する最近傍のデータが識別において重要な意味を持ち、このデータのことをサポートベクターといいます。これがサポートベクターマシンの名前の由来になっているんですね。
またマージンはある境界を設定した場合にその境界がどれだけ近傍のデータから離れているかを示します。線形識別関数のマージンをkとすると、全ての学習データにおいて以下の式が成り立ちます。
両辺をkで正規化してwとbをkで除したものとして置き直し、2値分類の正解ラベルの-1,1を用いて絶対値を外すと以下のように表現でき、
このときt=+1のデータで識別平面に最も近いデータは重みベクトルwの方向に射影した同一クラス内のデータの中で長さが最小となり、同様にt=-1のデータで識別平面に最も近いクラス内のデータは射影した長さが最大になります。
よってクラス間マージンは両クラスのデータを重みベクトルwの方向へ射影した長さの差の最小値、つまりt=+1クラスの射影後の長さの最小値とt=-1クラスの射影後の長さの最大値の差、として以下のように与えられます。
サポートベクターマシンではクラス間マージンを最大化することで識別境界を決定するため、上記の式を最大化するには||w||を最小化することで求めることができ、つまり以下の不等式製薬条件最適化問題の主問題を解くことでサポートベクターマシンの学習を行うことができるんですね。
最小化:
不等式制約:
制約付きの関数の最大化、または最小化を扱う手法にラグランジュ未定乗数法があり、サポートベクターマシンでもこの手法を利用します。先ほどの問題をラグランジュ関数にしてみましょう。すると以下の式になります。
ここで導入された\alphaはラグランジュ乗数といいます。この最適化問題の解はKKT条件を満たす解として与えられます。そしてそのKKT条件が以下の通りで、
ラグランジュ関数に2つ目のKKT条件を代入すると、
のようになり、最適解が学習データの線形結合で表現され、係数\alpha_iを求める問題と考えることができます。この最適な\alpha_iはラグランジュ関数を最大にする\aplha_iであり、これを主問題に対して双対問題といいます。
先ほどの式を少しまとめるとこの双対問題は以下のように定式化でき、
最大化
等式制約条件
この双対問題を解くことで最適な\alpha_iを求め、それをKKT条件に代入することで\vec{w}、bを求めることができます。
まとめ
SVMについて重要な点をまとめましょう。
- 識別境界を決定するのに重要なサポートベクターを用いてマージンを最大化するよう学習する手法
- カーネル関数を用いて非線形な問題も対応できる
- 数学的に綺麗に問題を解くことができるため、人気があった




