RMSEを楽々理解！二乗平均平方根誤差を実装しながら学ぼう

最近のAI人気の高まりから少し機械学習を勉強すると、誤差関数で様々な数式が出てきて難しく感じることがありますよね。本記事ではその誤差関数として最も有名なもののひとつである、Root Mean Squared Error; RMSE 日本語で二乗平均平方根誤差について説明していきます。

先ほども述べたとおりRMSEは最も有名な誤差関数のひとつで、分類と回帰でいうと回帰問題を解く場合によく利用されます。そのRMSEについて実装しながら他の誤差関数とはどのような違いがあるのかをみていきましょう。

分類問題は犬か猫のうちどちらかといった識別を行う問題で、回帰問題は家の値段は何円だといった値を直接予測する問題のことをいいます。

RMSE(二乗平均平方根誤差)とは
RMSEの使い所
RMSEをPythonで実装してみる
まとめ

RMSE(二乗平均平方根誤差)とは

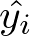
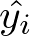
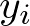
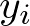
RMSEとは以下の数式で表される誤差のことで、予測と値がどの程度離れているのかを評価する関数です。 $\begin{align*} \hat{y_i} \end{align*}$ が機械学習モデルの予測した値で、 $\begin{align*} y_i \end{align*}$ が実際の正解データとなります。

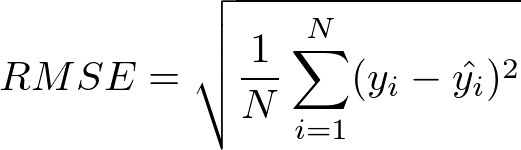
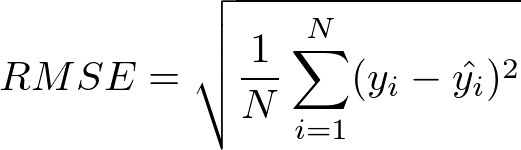
この数式がどういう意味を持つのかを説明すると以下の点が言えます。

合計N個のデータに対して、予測と正解の差を計算する
その差を2乗してから平方根を取ることで値のスケールを戻している

これをもう少し易しく言い換えると以下のような表現ができます。

機械学習モデルの予測値がどれだけずれているかを図る指標
予測を少しだけ外したものよりも、大きく外したものについてより罰則を与えるような評価をしている

RMSEの使い所

一般に機械学習は設定した誤差関数を最小にするように学習を進めていきます。そのため回帰問題を解く際の誤差関数をRMSEに設定し、モデルの予測と正解のデータから計算されたRMSEが最小になるようにモデルを学習させるといった使い方をします。

またモデルが正解データに対してどれだけ真っ当な予測を出来ているのかを評価するのにもRMSEを用います。モデルに変更を加えた際にRMSEの値を計算して、先ほどよりも小さくなっていればモデルの改良に成功したと考えられ、逆にRMSEの値が大きくなっていた場合は予測の精度が先ほどよりも悪化してしまったと考えることが出来ます。

RMSEをPythonで実装してみる

今回コードを実行した環境は以下の通りです。

Python 3.7.3
NumPy 1.18.1

実装したコードが以下になります。

NumPyというPythonの数値計算に特化したライブラリを用いました。

import numpy as np


def root_mean_squared_error(y_true, y_pred):
    mse = np.power(y_true - y_pred, 2).mean()
    return np.sqrt(mse)


if __name__ == '__main__':
    y_true = np.array([10, 20, 30, 40])
    y_pred = np.array([10, 10, 10, 10])

    rmse = root_mean_squared_error(y_true, y_pred)
    print(f'rmse: {rmse}')
    # 実行結果は
    # rmse: 18.708286933869708

root_mean_squared_errorという関数でRMSEを計算できるようにしました。本コードではその関数に擬似の正解データy_trueと擬似の予測データy_predを入れて、RMSEの値を計算させて計算結果を表示しています。

AI開発の際はこういった評価指標をあらかじめ定めて、この値をなるべく改善していくようにデータサイエンティストたちが日々格闘しています。また評価指標選びも重要で目標を達成するために、なるべく適した評価指標を選べるようになることもデータサイエンティストとしての腕の見せ所となります。