機械学習を学ぶなら知っておきたい！partial dependence plotとは

機械学習モデルの予測に関する解釈手法には様々な手法が存在していますよね。本記事ではそれぞれの特徴量が予測にどのような影響を与えるのかを知るための手法である、Partial Dependence Plot(パーティアル デペンデンス プロット)について解説しましょう。

機械学習の解釈とは

Deep Learningのような予測に必要な内部のパラメータが多いモデルでは、入力がどのように出力されるのかを人間が理解するのは難儀ですよね。そこで何か別の手法を用いてモデルの挙動を把握するために機械学習の様々な解釈手法が研究されています。

本記事で紹介するPartial Dependence Plotはある特徴量が変化したとき、どのように予測に影響を与えるのかを評価します。これによって人間の直感と一致しているかを確認することができ、学習させたモデルの理解の助けになります。

Partial Dependence Plotの仕組み

まずはscikit-learnを（サイキットラーン）用いて実際にPartial Dependence Plotの図を出力してみましょう。データセットにはirisデータセットを用い、学習モデルにはGradient Boosting Decision Tree（グラディエント ブースティング ディシジョン ツリー）を利用しました。

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.inspection import plot_partial_dependence

X, y = load_iris(return_X_y=True)
model = GradientBoostingClassifier(n_estimators=10, max_depth=1)
model.fit(X, y)
features = [0, 1, 2, 3]
plot_partial_dependence(model, X, features, target=2)
plt.show()

このスクリプトを実行することで以下の結果が得られました。

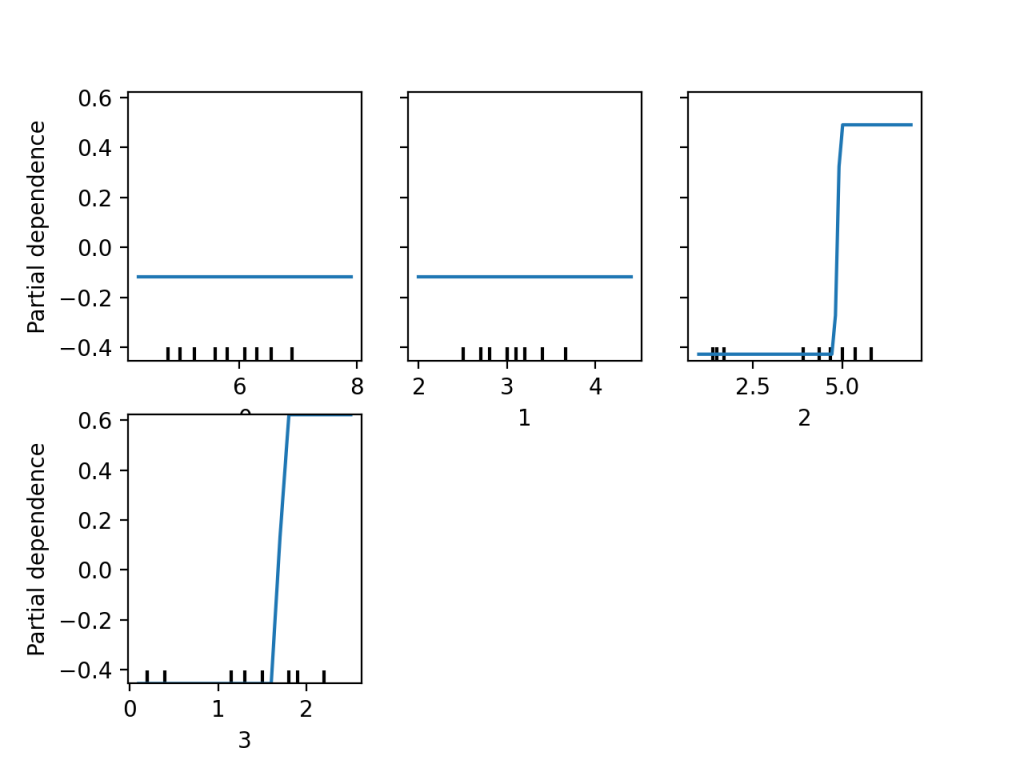
このプロットではirisデータセットに存在する4つ全ての特徴量に関してPartial Dependenceを計算しています。またtargetに2設定しており、これはアヤメの種類の中でvirginicaというラベルを予測する際の特徴量と出力の差を計算するように指定しています。

特徴量0と特徴量1のプロットは特徴量の値が変化しても、予測にはほとんど影響がないことを示しています。しかし特徴量2は5.0あたりからPartial Dependenceの値が非常に大きくなっており、同様に特徴量3では1.5を超えたあたりからPartial Dependenceの値が大きくなっていることがわかりますよね。これはこれらの特徴量が一定の値を超えた場合に答えがvirginicaであると予測しやすいことを示しています。

次はtargetに0を指定してみましょう。アヤメのsetosaというラベルの予測に関するPartial Dependenceを計算することになります。計算結果が以下のグラフです。

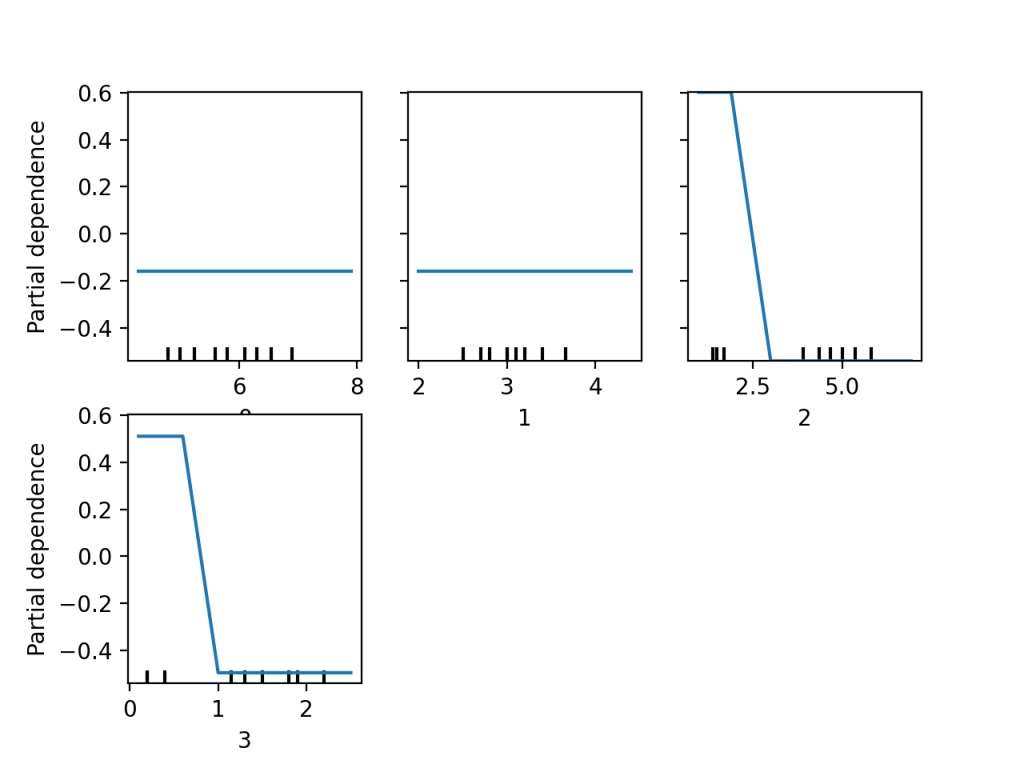
上記プロットから、setosaにおいても特徴量の0と1はほとんど影響をもたらさないようです。また特徴量2と3は値が小さいほどsetosaであると予測しやすいことを示しており、先ほどのプロットも考慮して、特徴量の2と3が小さいほどsetosa、大きいほどvirginicaと予測するモデルであると考えることができます。

まとめ

Partial Dependence Plotについて重要な点をまとめましょう。

• 機械学習モデルの解釈手法のひとつ
• ある特徴量が予測にどのような影響を与えるのかを可視化できる
• scikit-learnで簡単に実装できる