線形回帰モデル入門！ゼロからわかる機械学習アルゴリズム

「線形回帰」という単語はAI（機械学習）を学び始めた人ならば誰しも出会う言葉ですよね。しかし、コード一行で線形回帰の処理は完了してしまうので具体的な理解が曖昧になっている人も多いかもしれません。線形回帰の具体的理解は、機械学習を応用していく上で基礎になる部分であり非常に重要です。そこで今回は線形回帰について整理して行きます。

一言で言うと「線形回帰」とは・・・

データからデータの傾向やパターンを上手く表現する

という数式を求めること

つっちー

もちろんこれだけでは理解できないので以降で順番に説明していきます。

最も単純な線形回帰は直線

線形回帰について見ていく前に、そもそも「回帰」とは、正解となる数値と入力データの組み合わせで学習し、未知のデータから連続値を予測することです。

※連続値・・・1.1や1.01のように繋がった値をとれるもののこと。時間や速度など

回帰モデルは連続値をとる目的変数（求めたいもの）を予測するために使用されるので、例えば企業の今後の売上予測したり、明日の気温は何度かな？のような気温の予測などに適しています。

※モデル：数式で「事象を簡単にして本質（データのパターンやルール）を表したもの

単純な線形回帰から理解するとわかりやすいので具体例で考えてみましょう。例えば、自分が「愛の深さ研究家」だったとして、夫婦間における愛の深さを予測したいとしましょう。めちゃくちゃ話を簡単にして進めていきますが、道端で出会った夫婦に聞き取り調査をしまくったとします。

こんな感じで↓

・

・

・

（この例えについてはみなさん色々思うところがあるかもしれませんがご勘弁ください）

すると、愛の深さとその夫婦の結婚年数の関係は次のようにグラフにプロット（図の上に天をとること）できそうですよね。

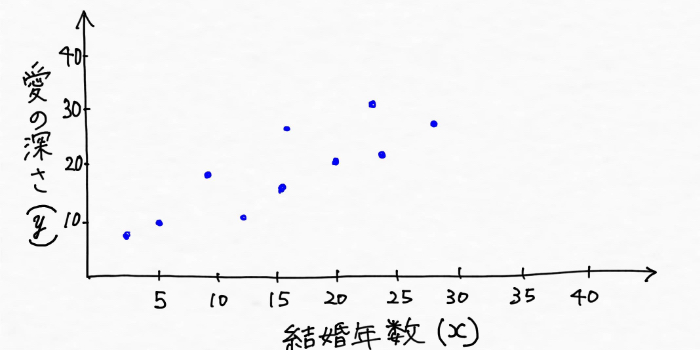
愛の深さと結婚年数という二つのデータには、ある一定のパターンがあることが見えてきました。次のように直線を引けそうです。

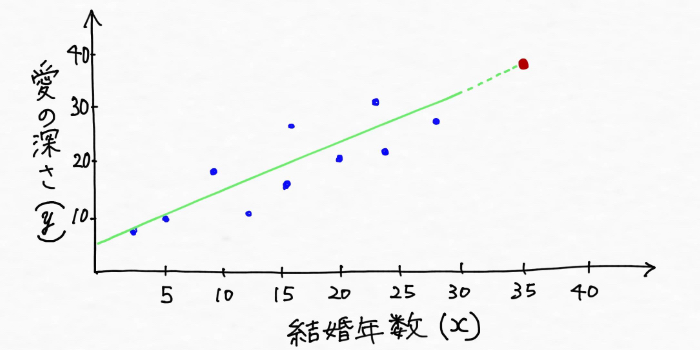
一度線を引いてしまえば、結婚年数がわからないカップルについても、大体の愛の深さを予測することができるようになりますよね。

※上図を使えば未知のデータである結婚年数35年のカップルの愛の深さについても予測できそうです

直線を引いたということはこれは数式で表現できるということですので、求めたいものである愛の深さをy、結婚年数をxとすれば、結婚年数x年のカップルの愛の深さは

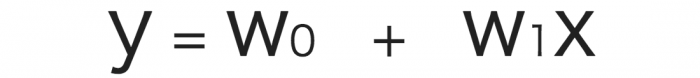
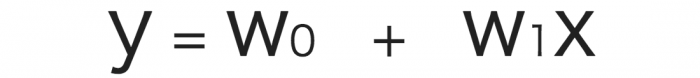
で表現できそうです！

※w0とw1 にはそれぞれ何らかの一定の数字が入ります

この数式こそが線形回帰モデルであり、この例では線形回帰モデルはデータの傾向、パターンをつかんだ直線を引くことで愛の深さと結婚年数の関係を表現しています。つまり線形回帰モデルは、愛の深さyと結婚年数xの関係を示す数式を表現する適切なw0とw1をデータから見つけていくということです。

AI（機械学習）の分野では求めたいものを「目的変数」、目的変数に作用する変数を「説明変数」と表現し、つまりこの例では

となります。

結婚年数から愛の深さを上手く予測できそうでしたが、現実ではこのように一つの説明変数（結婚年数）から目的変数（愛の深さ）を予測できるような問題はほとんどなく、目的変数を求めるためには様々な説明変数を考慮する必要が出てくるでしょう。

例えば、先ほどの例について愛の深さ（目的変数）に作用する説明変数として「結婚年数」の他に「キスの回数」があるとしましょう。つまり、愛の深さには「結婚年数」と「キスの回数」という二つの説明変数が作用するということです。

この時、目的変数である「愛の深さ」yは、説明変数である「結婚年数」xと「キスの回数」x1を用いて、

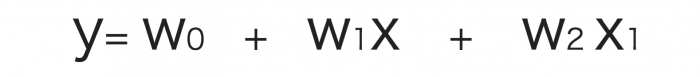
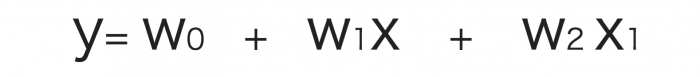
と表現できそうです。

※結婚年数xとキスの回数x1はカップルによって変化する変数で、w0、w1、w2にはそれぞれ何らかの一定の数字が入ります

これは全て例え話をしているので、実際愛の深さに対して「結婚年数」が強く作用しているのか、「キスの回数」が強く作用しているのかはわかりません。もし「結婚年数」xの係数w1が大きくなればそれはつまり「結婚年数」が愛の深さに作用する影響が強いということで、逆に「キスの回数」x1の係数w2が大きくなればそれは、キスの回数の作用の影響が強いということになります。

w1やw2など説明変数の係数は、説明変数が目的変数に与える影響度合いに寄与するものであり、機械学習の分野では「重み」と呼ばれます。

また、愛の深さ（目的変数）に作用するもの（説明変数）として「結婚年数」に加えて「キスの回数」が加わったように、実際には他にも「ハグした回数」、「ありがとうを伝えた回数」、・・・など様々な要素（説明変数）が愛の深さには関わって来そうですよね。

こんな風に実際はどれだけの説明変数（パラメータ）が関わってくるのかがわからないので、説明変数がm個あるとして線形回帰モデルを表現すると、、

となります。

※x0＝1としてy軸の切片を表しています

これが線形回帰モデルを一般化した数式です。

説明変数が一つだけだった時は線形回帰モデルは直線の形をしていましたが、説明変数が増えれば増えるほど線形回帰モデルはどんどんグニャグニャに複雑になっていくでしょう。データを適切に表現できる線を引くということはつまり、適切な数式を求める＝適切な重みを求める、ということになります。

※正則化された線形回帰については下記でご紹介しています。興味のある方はどうぞ

リッジ回帰／Lasso回帰／Elastic Net

AI（機械学習）を学び始めると「リッジ回帰」や「Lasso回帰」、「Elastic Net」などの単語を見かけますよね。こうした単語による処理はコード数行で実行できますが、中身を理解しなければ決して使いこなせません。そこで今回はこれらの基本と特徴、どのようなものであるかついてお伝えしていきます。

aizine.ai

まとめ

つまり、線形回帰とは

データからデータの傾向やパターンを上手く表現できるという数式を求めて、求めた数式を用いて未知のデータから連続値を予測することです。

＜参考＞

・Andreas C. Muller and Sarah Guido　(2016).　Introduction to Machine Learning with Python: A Guide for Data Scientists.　O’Reilly Media, Inc.　（アンドレアス・C・ミューラー、サラ・グイド　中田 秀基（訳）(2017).　Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎　株式会社オライリー・ジャパン）
・Sebastian Raschka(2015). Python Machine Learning. Packt Publishing. (株式会社クイープ、福島真太朗（訳）) (2016). 『Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)』

・松尾 豊(2015, 西林 孝(2018).『仕事ではじめる機械学習』株式会社オライリー・ジャパン.

・Aurélien Géron (著), 下田 倫大 (監修), 長尾 高弘  (翻訳) (2018). 『scikit-learnとTensorFlowによる実践機械学習』

つっちー

AI（人工知能）って「なにそれ美味しいの？」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください（実話）。