すぐわかるk近傍法！KNN(k-nearest neighbor)をPythonで実装しよう

巷を賑わす機械学習には様々な学習アルゴリズムがありますよね。学習アルゴリズムは用途に応じて使い分けられていますが、今回はその中でも非常に単純かつ強力なk近傍法(k-nearest neighbor)についてご紹介します。

また解説だけでなくPythonという言語を用いた実装を行うことで、より理解を深めていきましょう。

k近傍法（ケイきんぼうほう）とはどういうアルゴリズムなのか
k近傍法のメリット・デメリット
1. メリット
2. デメリット
Pythonによるk近傍法の実装
1. k近傍法モデルの実装
2. k近傍法を用いたアヤメの分類
まとめ

k近傍法（ケイきんぼうほう）とはどういうアルゴリズムなのか

この節ではk近傍法（ケイきんぼうほう）がどのように学習や予測を行うのかに関して説明していきます。簡単に説明するとk近傍法というのはその名の通り、あるデータに着目した時に近隣k個のデータの平均もしくは多数決の値を予測として出力するアルゴリズムです。

文字だけではイメージがつかないと思いますので、以下の図を用意しました。赤と青の2つのグループがあり、緑の点がどちらのグループに属しているのかを予測したい場合を考えてみます。

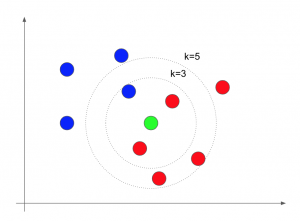
図1 k近傍法のイメージ

まずはk=3の場合を考えましょう。緑の点から緑の点自身を除く3点が入るように円を描きます(図1中の内側の円)。このとき赤の点が2つ、青の点が1つとなり、多数決の結果、予測値は赤であるとします。

次にk=5の場合を考えると(図1中の外側の円)、赤の点が4つ、青の点が1つとなり、k近傍法アリゴリズムでは赤と予測します。

k近傍法のkの値は人間が決めるべきハイパーパラメータであり、一般的には交差検証法などを用いて、精度が高くかつノイズに強くなる値を決めることになります。

k近傍法のメリット・デメリット

k近傍法のメリットとデメリットについては、ざっくりと以下のようなことがいえます。

メリット

精度が悪くない
非常に直感的でブラックボックス的な予測ではない

デメリット

毎回学習データの数だけ距離の計算を行うため、計算量が大きい
入力データの次元数が大きくなると、精度が出ない

k近傍法は近隣の点から予測を行うため、データの次元数が大きすぎないうちは精度もよく、また近隣k点の平均を予測値とするなど予測に関しても非常に直感的で人間が理解しやすいというメリットがあります。これは基本的に予測がブラックボックスと言われることの多い機械学習の分野ではk近傍法に特有の点となっています。

続いてデメリットをご紹介しましょう。

デメリットとしては、一般に予測1つごとに最も近い点をk個探すために、学習データ全ての点との距離を計算する必要があり予測1つあたりの計算コストが大きいという点があります。学習データの数を減らすと計算量は下がりますが、予測の精度も下げることになり、この辺りのトレードオフをどう調整するかという難しさもあります。

またもう1つのデメリットとして次元が大きなデータに対してはk近傍法はあまり有効でないという点も無視できません。データの次元が大きくなると次元の呪いの影響で、近傍と遠傍に距離の大きな差が出なくなり、精度が思ったより出ないということが起こりえます。

Pythonによるk近傍法の実装

本節ではpythonによるk近傍法の実装とそれを用いた学習と予測を行います。プログラムに詳しくない方は本節を読み飛ばしていただいても構いません。

今回のサンプルプログラムを動かした環境は以下の通りです。

Python 3.7.3
NumPy 1.18.1
Scikit-Learn 0.22.1

k近傍法モデルの実装

k近傍法をKNNという名前のクラスで実装しました。

今回実装するk近傍法では、距離にはユークリッド距離を用いています。ユークリッド距離以外にはマハラノビス距離などもよく利用されます。

学習はfit、予測はpredictという関数を用いて実行します。

import numpy as np


class KNN:

    def __init__(self, k: int = 5):
        """
        Args: 
           k (int): k個の近傍点から予測を行う。
        """
        self.k = k
        self.X = None
        self.y = None

    @staticmethod
    def euclidean_distance(m, n):
        """ ユークリッド距離の計算を行う関数。
        Args:
            m, n (np.ndarray): 距離の計算を行う2点。
        """
        return np.sqrt(np.power(m - n, 2)).mean()

    def fit(self, X, y):
        """ 学習を行う関数。
        Args:
            X (np.ndarray): 入力データ
            y (np.ndarray): Xに対する正解のデータ
        """
        if X.ndim != 2:
            raise ValueError(f'X.ndim must be 2, but got {X.ndim}')

        self.X = X
        self.y = y
        return self

    def predict(self, X):
        """ 学習完了後、予測を行う関数。
        Args:
            X (np.ndarray): 予測を行いたいデータ
        """
        if (self.X is None) or (self.y is None):
            raise ValueError(f'{self} is not fitted.')

        y_pred = []
        for x in X:
            distances = []
            for x_train in self.X:
                distance = self.euclidean_distance(x, x_train)
                distances.append(distance)
            # Get indices of nearest neighbors.
            indices = np.argsort(distances)[:self.k]
            # Make prediction!!
            y_pred_iter = np.mean(self.y[indices])
            y_pred.append(y_pred_iter)

        return np.array(y_pred)

k近傍法を用いたアヤメの分類

先ほど実装したKNNクラスを用いて、アヤメの分類を行います。

import numpy as np
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

from k_neighbor import KNN

if __name__ == '__main__':
    # アヤメデータセットの取得
    X, y = load_iris(return_X_y=True)
    # 入力データXに対する標準化の実行
    X = StandardScaler().fit_transform(X)
    # データを学習用と評価用に分割
    X_train, X_valid, y_train, y_valid = train_test_split(X, y, shuffle=True, random_state=27)

    # 近隣5点で多数決を行うKNNクラスのインスタンス化
    model = KNN(k=5)
    # 学習
    model.fit(X_train, y_train)
    # 各クラスの確率を予測
    y_pred_proba = model.predict(X_valid)
    # 確率の最も大きいクラスを予測とする
    y_pred = np.round(y_pred_proba)
    # 正答率の計算と表示
    acc = accuracy_score(y_valid, y_pred)
    print(f'Accuracy: {acc}')