AI（機械学習）が注目され始めてから何年も経ちますが、機械学習に関係の深い「GMM」というワードを見聞きして「ああGMMね」なんて思える方は非常に少ないはずです。それもそのはず、GMMは統計学や機械学習を仕事でゴリゴリに使うような人たちが使うような専門用語だからです。
僕自身はこのGMMというワードに最近初めて出会ったのですが、最初は何が何だかさっぱりでしたし、なになに？ゼネラルモーターズの何か？ぐらいに思ったほどです。
ひょっとするとこの記事を読みにきてくださった方には、僕と同じような思いをされた方が多いのかもしれません。今回はそんなよくわからないGMMについて整理していくことにしました！
そもそもなぜGMMを調べて記事にしようなんて思いついたのか
本章では個人的に僕の日常を書いてて結構脱線しているので、「結論は何なんだよ？結論は！！！」という方は読み飛ばしてください。。（長文です）
機械学習を用いてデータ分析の腕を競い合う有名な場があります。その名もKaggle！！僕はこのKaggleで上位入賞者に与えられるメダルを獲得した上で以前クビになった会社へ押しかけ＆直談判することで、AI（機械学習）エンジニアとしてデビュー！という作戦をモチベーションに僕は日々を過ごしています。
先日もKaggleのコンペティションに参加していましたが、最終的に1839チーム中194位という成績で残念ながらメダルには届きませんでした。
1839チーム中194位って結構いいんじゃないの？って思われる方もいらっしゃるかもしれませんけど、これは機械学習の達人たちが書いたコードをコピペして来て、それをベースに自分なりに少し工夫して提出した内容の結果な訳で、やっぱり自分の実力だと明言するのは厳しすぎます。
コンペ終了後、高得点を出した強者たちがシェアする解法（コード）を見ていると、このコンペで高得点を叩き出すにはGMMを使うことが鍵だとわかってきたんですよね。
けれど、GMMなんて初めて聞いたワードで「GMM？何それ、おいしいの？」って感じでしたが、これを理解せずして凄腕の猛者たちと戦っていくこと、ましてやメダル獲得なんてできません。
そこでなんとかしてこのGMMを理解したかった僕はすぐさまググったわけですが、出てくるのは難しい数式や難解な言葉ばかり。困った末にお多福ラボ（僕が以前クビになった会社）で働く二人のエンジニアの顔が思い浮かんで彼らに聞こうかとも思ったのですが、、、
※登場人物紹介はこちら
やっぱり他人に時間をとってもらって教えてもらうっていうのは僕にとってみたらハードルが高いんですよ（><）聞いたら速いってことはもちろんわかってるんですけど、どうしても一歩を踏み出すのにはエネルギーがいるわけで・・・。「他人に迷惑をかけるな」って小さい頃から言われて来てその意味を捉え違えているというのは重々承知しているつもりなんですが・・・。
しかもつながりがあるとはいえ前の職場の社員に連絡するのは結構勇気が要ります 汗
加えて、やらさんに相談すると毎回「ふ」からはじまるサービスに行きたいからって見返り求められるし、シリルはいつも女の子追っかけてて忙しいからって中々取り合ってくれないっていうのも影響しているかもしれませんw
そんなわけでなんやかんや悩んでいたんですが、Webでよくわからない、他人に頼れない、それなら書籍じゃいっ！！と、何か良さげな本はないかと調べていったところ、ありました。。僕はこの本を見つけました（アマゾンで）。
『見て試してわかる機械学習アルゴリズムの仕組み 機械学習図鑑』
見つけたはいいんですがリアルな話をすると、僕はこの本を購入するのを一瞬渋りました。・・・なぜなら書籍代の3000円が金銭的に苦しかったからです。。
少し背景を暴露すると、全然使いこなせないのに一丁前にカスタマイズして30万円近くになってしまったPCの支払いローンや、学ぶこと自体が目的で（痛い >_<）昔いくつか通っていたAIスクールの出費（結構な金額ですよコレ）、そして引越しなども重なって（まあ昔の話ですが）もう僕の財布はマイナスです。
つい先日29歳の誕生日を迎えたばかりですが、親に借金までして目標を追いかけてる始末なわけで、将来的に稼げるようになって倍に返せればいいやと思ってここまで勢いで走り続けて来ましたが、何の保証もなくてやっぱり不安になりますよ。書いてて本当に恥ずかしいです。（てかよく書いたなこんな内容 汗）
なんで貯金してこなかったの？って声が聞こえそうですが、過去に自己啓発書マニアと言われ新卒入社した会社で自己啓発書を禁止されたぐらいの僕は、貯金は一切せずに書籍やセミナー参加、あとは六本木ヒルズの会員制コミュニティなどなどに入会したりして、持ち金全てを自分へ投資して来ました。あとは自炊する時間がもったいないとかって100%外食したりしてきたので、数年間ガスコンロを使わない生活をして来ました（今は違います）。
まあ、完全に僕のお金の管理の甘さに全ての原因があるわけなんですが。。トホホ・・・。
だからこそ、書いてて恥ずかしいですがリアルな話、自分に余裕がなくて約3000円の書籍を購入して良いか迷ったわけですね。ただ、やっぱり自分への可能性を諦めたくないですし、自分に投資できないということ＝自分への可能性を諦めている ことだと思ったのでここは自分へ投資するんじゃいっ！という考えで思い切って書籍を購入しました。
と、ここまで話が長くなりましたがこんな背景があって、今回はGMMについて書籍『見て試してわかる機械学習アルゴリズムの仕組み 機械学習図鑑』とWebで僕が理解できたところを踏まえて「GMM」って何？を記事にまとめることにしました！！
GMMとは何なのか？
調べてみると、GMMとはGaussian Mixture Model：混合ガウスモデル（ガウス混合モデル）と呼ばれるもので、クラスタリング(※)の一つに当たるようです。具体的には、どのようにデータ点が分布しているかのパラメータを推定する手法ということですが、この表現ではまだまだわからないので順番にここから整理していきましょう。
これを理解するには「ガウス分布」と「混合ガウス分布」をしっかり押さえておく必要があることがわかったのでまずはこの二つを順番に整理していきます。
※クラスタリング：データ間の距離に基づいて類似するデータをグループに分ける手法
まずはここから！ガウス分布と混合ガウス分布
まず、統計学や機械学習においてよく利用されている確率分布(※)にガウス分布（正規分布）があります。左右対称で平均付近に一番データ点が集まっている次のような分布がガウス分布です。
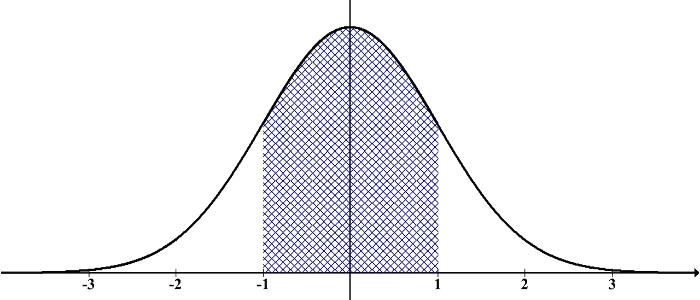
このガウス分布は、データがどこを中心としたものかを表す「平均」と、どのくらいばらついているのかを表す「分散」という二つのパラメータ（変数）によって、データの分布を表現できる性質があります。
※確率分布：ざっくりいうとヒストグラムを割合で書き直したもの
※分散：データ点と平均の差の2乗の平均
ちなみに、ほとんどの機械学習モデルは個々の特徴量（データにどのような特徴があるかを数値で表現したもの）がだいたいガウス分布に従っているときに最も上手く機能するという前提があります。
そしてこのガウス（正規）分布を次のように複数重ね合わせた（線形重ね合わせ）もの、言い換えれば混ぜ合わせたものが混合ガウス分布と呼ばれるもので、
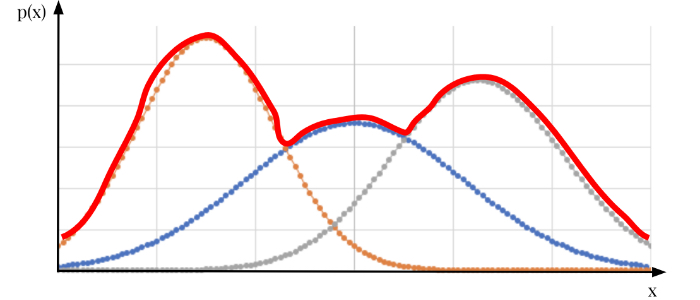
※わかりやすいように一次元のデータで表現しています
この混合ガウス分布を用いてどのようにデータ点が分布しているかのパラメータを推定する手法がGMM（Gaussian mixture models：混合ガウスモデル）です！（この表現はまだまだわかりづらいので順番にここから整理していきます）
GMM（混合ガウスモデル）はデータ点が属しているガウス分布を確率で表現する
先ほどガウス分布は「平均」と「分散」という二つのパラメータによって表現できると書きましたが、GMM（混合ガウスモデル）を用いて各データ点の分布のパラメータを推定できればその推定したパラメータを元に、あるデータ点がどんなガウス分布に属しているかを推定できるというわけです！
もちろん、「このデータ点はこんなガウス分布に属しているだろう」なんて推定しても、データ点が実際推定通りであるかどうかはわかりません。そこでGMM（混合ガウスモデル）は「こんなガウス分布に属しているだろう、答えは一つだ！」という決めつけるやり方はせず、「こんなガウス分布に属していると考えるのが確からしいなあ、何%の確率で属していそうだなあ」と柔軟に表現します。
あるデータ点が重ね合わさったガウス分布のうちのどれに属しているかを確率で表現するわけで、具体的には「このデータ点はガウス分布Aには70%の確率で属しているだろう」、「ガウス分布Bには30%の確率で属しているだろう」、「ガウス分布Cには10%確率で属しているだろう」。。というように考えます。
ちなみにAI（機械学習）を学んでいてよく出てくる「予測」と「推定」という言葉はごっちゃにしてしまいがちですが、次のように異なる意味があります。（調べました）
※予測：未来時点のある値を現時点の情報から算出すること
※推定：現時点の一部の情報を利用して現時点の全体の値を算出すること
ハードクラスタリングとソフトクラスタリング
ここで気づいた方もいらっしゃるかもしれませんが、GMM（混合ガウスモデル）はデータ点が全てガウス分布で存在していることを前提としているため、データ点の分布がこの前提に沿わない場合はうまく機能しません。また、n個のガウス分布がある時各データ点はいずれかのガウス分布に割り当てられる、つまりクラスタ（正規分布）もn個あるということを前提としています。
改めて、GMM（混合ガウスモデル）のようにグルーピングを行う処理はクラスタリングと呼ばれますが、GMM（混合ガウスモデル）によるクラスタリングは一つのデータ点が複数のガウス分布のどれに属するかを表現するという意味で柔軟な形を取っています。このようなクラスタリング方式はソフトクラスタリングと呼ばれています。
対照的に、一つのデータ点を一つのクラスタに割り当てるクラスタリング（k-meansなど）はハードクラスタリングと呼ばれるもので、つまりクラスタリングには堅いもの（ハード）と柔らかいもの（ソフト）があるというわけですね(^^)
k-meansをはじめとしたハードクラスタリングについては以前整理したことがありますので、気になる方はこちらをご覧ください。
GMMのアルゴリズムはどうなっているのか？
GMM（混合ガウスモデル）による学習では、与えられたデータ点から各ガウス分布ごとのパラメータ（平均と分散）を求めます。平均と分散が求められれば、与えられたデータ点がどのガウス分布に属しているかを推定できるからです。
GMM（混合ガウスモデル）の概要は掴めたのですが（僕が）、具体的にどういうアルゴリズムで動いているのかはわかりません。。。
そこで、ここからはわかりやすい一次元データで、GMM（混合ガウスモデル）がどうやってパラメータ（平均と分散）を求めるのかを整理していきます。
次の図は、２つのガウス分布とそれらのガウス分布から取り出した（サンプリングした）一次元データをプロットしたものです。
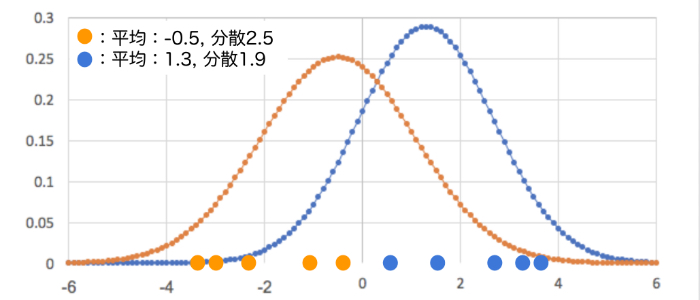
赤いプロットは、平均：-0.5、分散：2.5のガウス分布からサンプリングされたデータで、一方青いプロットは平均：1.3、分散：1.9のガウス分布からサンプリングされたデータです。
上図のように各データ点がどのガウス分布に属しているかを例えば色でわかるような状態なら、各データ点ごとに平均と分散を求めていけば良いので問題はたやすいでしょうが、そんな風に事前にどのガウス分布に属しているかなんて普通わかりません。
そのためGMM（混合ガウスモデル）では、データ点がどのガウス分布に属しているのか確からしいかを表す「重み」を推測した上で、データ点が属しているだろうガウス分布ごとにパラメータ（平均と分散）を推測していくことになります。
具体的には、以下の手順でガウス分布を決定するパラメータ（平均と分散）を求めます。
- 各ガウス分布のパラメータ（平均と分散）を初期化する（各ガウス分布の平均と分散を決める）
![混合ガウス分布]()
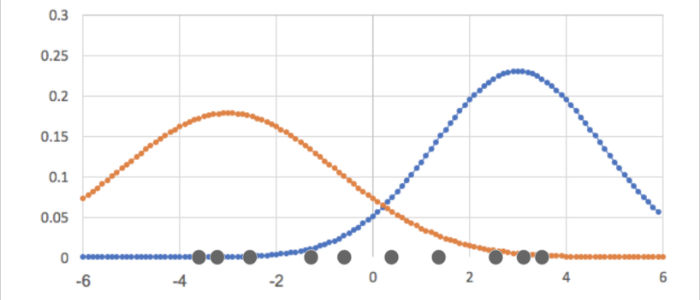
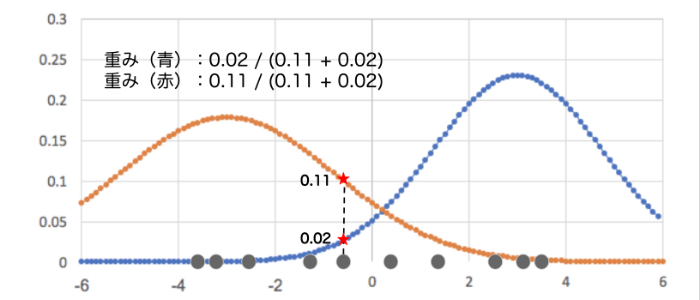
- データ点の重み（どのガウス分布に属しているかが確からしいか）を各ガウス分布ごとに計算する。
※重み ＝ 各ガウス分布の値 ／ 全てのガウス分布の値の合計。
※全データ点について重みが計算できたら各ガウス分布ごとに重みの平均を求め、次に分散を計算します。（平均とデータ点の差の２乗の重み付き平均を計算）![混合ガウス分布]()
- ②で得られた結果（重み）から、パラメータ（平均と分散）を再度計算する
![混合ガウス分布]()
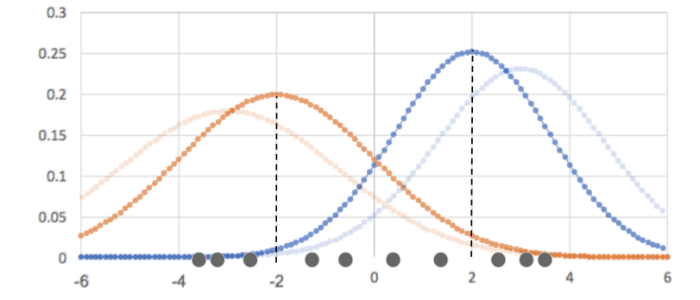
- ③で更新された各平均の変化がある基準（変化が十分小さい、規定の回数を超えた等）を満たすまで２と３を繰り返す
![混合ガウス分布]()
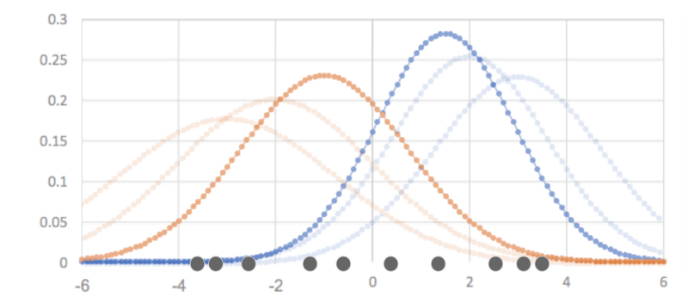
上図から、徐々に推定したガウス分布の形が変わっていくことがわかりますね！
このようにGMM（混合ガウスモデル）は、データ点がどのガウス分布に属しているかが確からしいかを重みで表現し、２と３の工程を繰り返すことで各データ点が属しているだろうガウス分布ごとにパラメータ（平均と分散）を更新していく手法です！
まとめ
さて、ここまでGMM（混合ガウスモデル）について理解を深めてきたわけですが、GMM（混合ガウスモデル）はクラスタリングの一つで、どのようにデータ点が分布しているかのパラメータを推定することで各データ点を複数のガウス分布の重ね合わせで確率を用いて表現することがわかりました（僕が）。
記事タイトルを振り返ってみると「GMMって何？混合ガウス（正規）分布を超わかりやすく理解するコツ♪」でしたが・・・・・これは完全に盛りすぎました本当にごめんなさい（テヘペロ♡）。
ただ、数式を使うと中々理解が追いつかなくなる僕が数式を使わずにGMM（混合ガウスモデル）を整理してみたので、僕のように数学は得意じゃないしGMM（混合ガウスモデル）ってなにそれ？、おいしいの？ みたいな方にとっては、初めの一歩として理解の手助けになったかもしれません（なっていてほしいです）。
今回は「わからない」から始まってGMM（混合ガウスモデル）という新たな武器の取り扱い説明書を読んで概要をざっくり掴んだわけですが、
「説明はいいから早く使ってみたら？使わないと本当の意味で理解できないし学んだ意味ないよ」
なんて声が聞こえてきそうですね 汗。
なので今後は機械学習を用いてデータ分析の腕を競い合うKaggleなどで、実際にGMM（混合ガウスモデル）を使って自分の血と肉としていくステップです。Kaggleに潜む猛者たちの実力に圧倒されながらも（ゴールドメダル、シルバーメダルはまだまだ遠いなと感じます）、少しずつ自分の技（機械学習プログラミング）を磨いてこれからもAI（機械学習）エンジニアの道へと繋げていきます！
＜参考＞
・秋庭 伸也 (著), 杉山 阿聖 (著), 寺田 学 (著), 加藤 公一 (監修) (2019)『見て試してわかる機械学習アルゴリズムの仕組み 機械学習図鑑』.翔泳社
・混合ガウスモデル (Gaussian Mixture Model, GMM)～クラスタリングするだけでなく、データセットの確率密度分布を得るにも重宝します～
・混合ガウス分布（GMM）の意味と役立つ例 – 具体例で学ぶ数学
・混合ガウス モデルによるクラスタリング
・統計的声質変換 (5) scikit-learnのGMMの使い方
・混合ガウスモデルとEMアルゴリスム
続く↓
AI（人工知能）って「なにそれ美味しいの？」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください（実話）。
コメントをどうぞ